LLaMA: Open and Efficient Foundation Language Models

(The LLaMA paper)

• Touvron, Lavril, Izacard et al (Meta)
• FEB 2023

Theory

LLaMA was inspired by the findings of Hoffman et al (2022), which took an opposite approach to predecessors like Brown et al (2020, OpenAI “LLMs are Few Shot Learners”) and Kaplan et al (2020) who focused on scaling up LLMs after finding their few-shot capabilities beyond a certain parameter threshold

Hoffman et al instead demonstrates that, for a given training compute budget, the best performance is not acheived by larger models but by more data.

Touvron, Lavril, Izacard et al introduce considerations for inference compute budgets, suggesting that even smaller models could be further saturated with even more data than suggested by Hoffman et al

Thus, LLaMA models were trained on over 7x the suggested number of training tokens per parameter and with 30% smaller size (for, presumably, the same budget)

LLaMA comes in 7B, 13B, 33B, and 65B parameter models, trained on 1024 Nvidia A100 GPUs over 1T (the 7B and 13B models) to 1.4T (the 33B and 65B models) tokens

- Most tokens are seen only once
- All data for training is open source (non-proprietary)

LLaMA 13B (and larger) models outperform GPT-3 on most benchmarks (despite being >10x smaller) but can be run on a single (large, over ~26GB VRAM) GPU

Architecture

Pre-normalization (GPT-3)

see Zhang and Sennrich (2019)

SwiGLU activation (PaLM)

see Shazeer (2020)

Rotary Embeddings (GPTNeo)

see Su et al (2021)

AdamW Optimizer

see Loshchilov and Hutter (2017)

Efficient Implementation

LLaMA uses an efficient implementation of the causal multi-head attention to reduce memory usage and runtime, by not storing attention weights or computing key/query scores that are masked (see Rabe and Staats, 2021, and Dao et al, 2022)

They also manually implement a backward function that stores expensive activations (some linear layer outputs) to avoid recomputation, rather than using autograd

This required reduced memory usage, using model and sequence parallelism (Korthikanti et al, 2022)

Despite (and perhaps because of) its relative density of training per parameter, LLaMA was shown to outperform existing fine-tuned models of comparable parameter size on MMLU (see Chung et al, 2022)

Attention Is All You Need

(The Transformer paper)

• Vaswani et al (Google Brain)
• JUN 2017

The transformer was originally designed to replace LSTMs, RNNs, and CNNs, drawing from their use of encoder/decoder attention mechanism

Self-attention, sometimes called intra-attention is an attention mechanism relating different positions of a single sequence in order to compute a representation of the sequence

Architecture

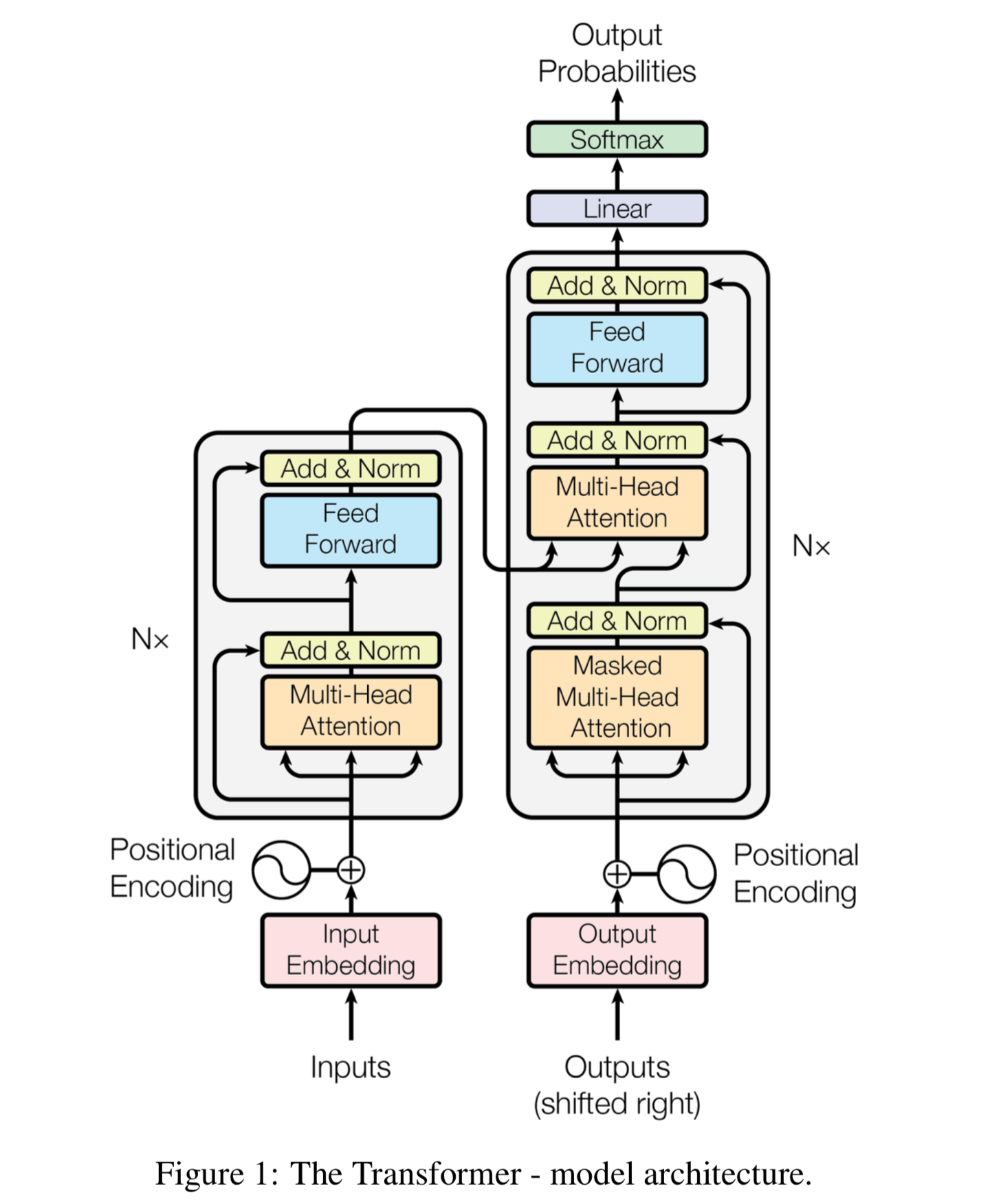
The encoder maps an input sequence of symbol representations $(x_1,…,x_n)$ to a sequence of continuous representations $\mathbf{z} = (z_1,…,z_n)$

The decoder uses $\mathbf{z}$ to generate an output sequence $(y_1,…,y_m)$ of symbols, one element at a time

Encoder

The encoder is composed of $N$ identical layers, each with two sublayers: a multi-head self-attention module and a fully connected feedforward network (MLP)

A residual connection, whereby the input sequence is added to the output sequence of the sublayer, and a layer normalization, whereby the aforementioned sum is converted into z-scores, are used around both layers:

To allow the residual connection, each sublayer and embedding layer has the same output dimension $d_{model}$

Decoder

The decoder is also composed of $N$ identical layers, each with an additional sublayer (between the original two) for multi-head attention over the output of the encoder stack

The first (original) multi-head attention sublayer is also modified (masked) to prevent positions from attending to subsequent positions

Attention

The attention module maps a query and a set of key-value pairs to an output, with the output being a weighted sum of the values, where the weight is based on the compatibility of the query with the corresponding key

Scaling the dot product by $\sqrt{d_k}$ prevents large values from pushing the softmax function into regions with extremely small gradients

- this value is chosen because it prevents the dot product variance from growing by $d_k$

in code:

## Define query, key, and value vectors
query = torch.randn(1, 8)  # (batch_size=1, query_length=1, embedding_size=8)
keys = torch.randn(10, 8)  # (key_length=10, embedding_size=8)
values = torch.randn(10, 16)  # (key_length=10, value_size=16)

## Compute the dot product of the query and key vectors
attention_weights = torch.matmul(query, keys.transpose(-2, -1))

## Scale the attention weights
scaled_attention_weights = attention_weights / torch.sqrt(keys.shape[-1])

## Normalize the attention weights using softmax along the key dimension
normalized_attention_weights = torch.softmax(scaled_attention_weights, dim=-1)

## Compute the weighted sum of the value vectors
output = torch.matmul(normalized_attention_weights, values)

print(output.shape)  # (batch_size=1, query_length=1, value_size=16)

Multi-head attention adds an additional dimension, $h$, to each input tensor (and thus each output tensor), then concatenates the output

Each head projects the $d_{model}$ Q (or K or V) into $d_{model}/h$ dimensions, where $h$ is the number of heads

The reduced dimensionality of each head means all $h$ heads require the same compute as a single-head with full dimensionality

in code:

import torch.nn as nn
import torch

## Define query, key, and value matrices
query = torch.randn(1, 10, 16)  # (batch_size=1, query_length=10, embedding_size=16)
keys = torch.randn(1, 12, 16)  # (batch_size=1, key_length=12, embedding_size=16)
values = torch.randn(1, 12, 32)  # (batch_size=1, key_length=12, value_size=32)

## Define the multi-head attention module
num_heads = 4
head_size = 8
multihead_attn = nn.MultiheadAttention(embed_dim=16, num_heads=num_heads, kdim=16, vdim=32)

## Apply multi-head attention to the input
output, _ = multihead_attn(query, keys, values)

## Concatenate the outputs of the different attention heads
output = output.transpose(0, 1)  # (query_length=10, batch_size=1, embedding_size=32)
output = output.contiguous().view(1, -1, num_heads * head_size)  # (batch_size=1, query_length=10, embedding_size=32 * num_heads)

print(output.shape)  # (batch_size=1, query_length=10, embedding_size=32 * num_heads)

Position-wise Feed-Forward Networks

Two linear transformations with an activation (in this case ReLU) between them:

The inner layer, in this case, has dimension $d_{ff} = 4 \times d_{model} = 2048$

Embeddings

The token embeddings of dimension $d_{model}$ are also learned

The same wieght matrix used for embeddings is shared with the linear layer after the decoder before the softmax that yields next-token probabilities

Positional Encodings

Positional encodings are added (literally) to the input embeddings before the encoder/decoder stacks to encode information about their position in the sequence

The details here are rendered basically irrelevant by the RoPE positional embeddings (see Su et al, 2021)

Training

The original transformer was trained on 8 Nvidia P100 GPUs, taking 12 hours for base models (65M) and 3.5 days for large models (213M)

They used Adam optimization with a linear learning rate scheduled warmup and step number inverse square root-proportional decay thereafter

Three [sic] types of regularization were used during training: Residual Dropout, and Label Smoothing

Updates

Since the original transformer paper, the typical architecture has changed

Some changes are merely differences in the optimizer, norm function, activation function, etc.

But a key change to the architecture is placing the layer normalization before each transformation, rather than after, alongside the residual addition (this is called the “pre-norm formulation”)

Further, dropout layers are sometimes added to prevent overfitting (see Srivastava et al, 2014)

From Karpathy’s video on GPT from scratch:

because the mask of what is being dropped out at every forward and backward pass, it ends up sort of training an ensemble of subnetworks, and when the training is complete and the dropout is removed, each of those subnetworks are merged

(Note: he mentions in the video, filmed in his living room, that he trained it on an A100 GPU lol)

He also clarifies that the “encoder-decoder” framework, which introduces cross attention (whereby second multi-head attention layer in the decoder gets its query and key matrices from the encoder output), is only used in sequence-to-sequence tasks, like translation, and not in purely autoregressive models, like GPT

RoFormer: Enhanced Transformer with Rotary Position Embedding

(The RoPE paper)

• Su et al (Zhuiyi Technology Co., Ltd., Shenzhen)
• APR 2021

Background

Traditional transformer model architectures use some (set of) function(s) $f$ to map a d-dimensional word embedding $x$ and position $m$ (or $n$) to query vectors (, key vectors, and value vectors)

recall that the query and key vectors are used to compute attention weights ($q_m^\top \cdot k_n$ normalized), and the output is computed as the weighted sum over the value vectors.

Previous Approaches

This $f$ typically takes the form of a trainable weights matrix $W$ multiplied by the sum of $x$ and some positional encoding $p$

Thus, $q_m^\top \cdot k_n$ could be rewritten as $f_q(x_m, m)^\top \cdot f_k(x_n, n)$ or $(W_q \cdot (x_m + p_m))^\top \cdot (W_k \cdot (x_n + p_n))$

In the original transformer paper, $p$ was a sinusoidal function depending on the parity of each token’s absolute position

More recent methods have made this $p$ value a trainable parameter to attempt to capture relative position information, but this massively complicated the model, making it incompatible with linear self-attention

These methods involved decomposing $(W_q \cdot (x_m + p_m))^\top \cdot (W_k \cdot (x_n + p_n))$

Rotary Position Embedding Approach

The RoPE paper attempts to formulate a function $g$ which accepts two word embeddings, $x_m$ and $x_n$, and their relative position, $m - n$, and outputs all information for $f_q$ and $f_k$ (specifically, their matrix dot product)

Rather than following the typical construction of $f$ as some $W \cdot (x + p)$, they find that $(W \cdot x_m) \cdot e^{i \cdot m \cdot \theta}$ with $\theta$ some constant solves for $g$

So $g$ is $Re[ (W_q \cdot x_m) \cdot \overline{(W_k \cdot x_n)} \cdot e^{i \cdot (m - n) \cdot \theta} ]$, a function of only $x_m$, $x_n$, and $m - n$, where $\overline{W_k \cdot x_n}$ denotes the complex conjugate of $W_k \cdot x_n$

Thus, our solution for $f$ only captures relative position differences (it yields the same answer without explicitly knowing $m$ or $n$)

In 2D, $(W \cdot x_m) \cdot e^{i \cdot m \cdot \theta}$ can be rewritten as $R \cdot W \cdot x$ for some rotation matrix $R$ of $m \cdot \theta$ degrees

In higher even dimensions $d$, we can divide the space into $d/2$ subspaces, such that every dimension is paired up with another dimension, so that the rotation matrix $R$ rotates pairs with respect to the plane they form

- this matrix looks like the 2D R stacked many times along the diagonal

Theta is chosen as a function of $d/2$ such that, as you move along the diagonal, $\theta$ decays exponentially: $\theta_i = 10000^{\frac{-2 \cdot i}{d}}$ (the same $\theta$ value proposed in the original transformer paper)

This has the characteristic that the matrix dot product $q_m^\top \cdot k_n$ will also decay as a function of $m - n$ (the relative distance)

It also is compatible with linear self-attention

Further Notes

They’ve also implemented a computational efficiency in calculating the rotation matrix by breaking the computation into two vector pairwise multiplications

They were able to demonstrate that they achieved lower loss at all training steps by incorporating RoPE into transformers currently using the traditional sinosoidal method

GLU Variants Improve Transformer

(The SwiGLU paper)

• Shazeer (Google)
• FEB 2020

Feed-Forward Networks (FFN)

During the feed-forward network in a transformer model, some vector x passes through two learned linear transformations (matrices W_1 and W_2) with an activation function applied between them.

In the original transformer model, this was a ReLU. Subsequent work proposed replacing ReLU with GELU and Swish

Non-Linear Activation Functions

The purpose of adding non-linearities to the model is to allow it to map non-linear distributions into shapes that can be linearly transformed into interpretable, low-dimension configurations

Typically, activations are designed to perform “zero-to-identity mappings” or shrinking small to negative values and maintaining large values.

GELU

GELU stands for Gaussian Error Linear Units and is written: $GELU(x) = x \Phi(x)$ where $\Phi$ is the cumulative normal CDF function

Pre-activations are roughly normally distributed, so $\Phi(x)$ is the probability that any new observation $X$ will be less than this particular observation $x$

So GELU scales each $x$ in proportion to the likelihood that it will be larger than other observed pre-activations.

Swish

Swish is a sigmoid approximation of GELU: $x \sigma (\beta x)$ (with $\beta$ typically $1.702$ for GELU approximation or $1$)

Swish is used because GELU is expensive to compute, and Swish has virtually identical characteristics

Bilinear

Bilinear activations use two parallel learned linear transformations ($W$ and $V$) and perform a Hadamard Product (pairwise vector multiplication) between the outputs

This Hadamard Product creates non-linearities because each component of a vector $x_w$ passed through $W$ is scaled by the corresponding value of another vector $x_v$ passed through $V$ (though a helpful interpretation, the actual implementation doesn’t privilege either $x_i$ vector, as the product is commutative)

Note that Bilinear activations require two learned linear transformation matrices, so comparisons in performance between bilinear and other activation functions require smaller learned linear transformation matrices to keep the model parameter size equal

GLU

GLU stands for Gated Linear Units

GLU performs a bilinear activation, but after first passing one of the vectors $x_v$ through another non-linear activation (originally the sigmoid activation)

This makes the scaling interpretation of the Hadamard Product more explicit: $x_w$ is “gated” by the activations of $x_v$

GLU Variants

GLU always works in conjunction with another activation function, so each of the above can be combined with GLU to replace sigmoid activation.

The naming conventions for each of the above activations used in GLU are: ReGLU (ReLU activated), GEGLU (GELU activated), and SwiGLU (Swish activated)

Performance

GEGLU and SwiGLU implementations of FFN outperformed all other activation functions in terms of heldout-set log-perplexity on pre-training

After fine-tuning on an array of benchmark performance tasks, GLU-variant activations continued to outperform other activations without bilinear activation (as well as simple bilinear activation itself)

From the paper:

We offer no explanation as to why these architectures seem to work; we attribute their success, as all else, to divine benevolence.

Searching for Activation Functions

(The Swish paper)

• Ramachandran et al (Google Brain)
• OCT 2017

This paper just compares the relative performance of various activation functions, determining Swish the highest performing

Decoupled Weight Decay Regularization

(the AdamW paper)

• Loshchilov and Hutter (University of Freiburg, Germany)
• NOV 2017

note: review of this paper is incomplete

Adam is a popular adaptive gradient method

Loshchilov and Hutter find that $L_2$ Regularization and weight decay, though possibly made equivalent by reparameterizing the weight decay factor based on the learing rate in the case of SGD, are not identical in the case of Adam optimization

Specifically, from the paper:

L2 regularization leads to weights with large historic parameter and/or gradient amplitudes being regularized less than they would be when using weight decay

Second, they find that, as a consequence of the above, $L_2$ regularization is not effective in Adam

Third, they find that optimal weight decay varies inversely to the total number of weight updates

Fourth, they find that Adam can substantially benefit from a global learning rate multiplier, scheduled by cosine annealing

Collectively, these improvements to Adam optimization are coined “AdamW”

LoRA: Low-Rank Adaptation of Large Language Models

(the LoRA paper)

• Hu and Shen et al (Microsoft)
• JUN 2021

Summary

LoRA freezes pretrained weights and injects trainable rank decomposition matrices into each layer of the transformer architecture

Compared to GPT-3 175B fine-tuned with Adam, LoRA can reduce the number of trainable parameters by 10,000x and the GPU memory requirement by 3x

The authors also observe a 25% speedup in tokens/s processing during training because the vast majority of parameters do not need their gradients calculated

LoRA also performs on-par or better than fine-tuning on most LLMs tested with no additional inference latency (unlike adapters)

Background

Traditional methods for more efficient fine-tuning involved adapting only some paramters to ease storage constraints, but these increase inference latency, total model depth, and often fail to match full fine-tuning baselines

For example, adapter tuning injects two fully connected layers with biases and an activation between them pretrained layers (or only after MLP modules with a layer norm, as in Lin et al, 2020)

Prefix-tuning methods consume an other-wise useful portion of the model context window (or add to it, thereby increasing inference latency)

Neural network dense layer matrices typically have full-rank, but, when adapting to a specific task, have low rank: they can be projected into smaller dimensionality without significant loss of information

Hu and Shen et al hypothesize that updates to those weights during pretraining thus also have low rank during adaptation.

Method

LoRA injects the rank decomposition matrices (initialized to a product of zero) alongside the frozen pretrained weights and sums them, so the inference model can simply merge the computed full-dimension matrix with the frozen weights by addition, without adding new parameters or layers to the model

For a pretrained weight matrix $W_0 \in \mathbb{R}^{d \times k}$ we define its update by $\Delta W = BA$ where $B \in \mathbb{R}^{d \times r}, A \in \mathbb{R}^{r \times k}$ for $r \ll min(d, k)$ (random Gaussian initialization for $A$ and zeros for $B$)

to perform a forward pass on input tensor $x$ we calculate $W_0x + BAx$

Empirical Studies

All empirical studies were performed on GPT-3 175B

Given a parameter budget constraint, which subset of weight matrices in a pre-trained Transformer should we adapt to maximize downstream performance?

Even for a parameter budget of 18M tokens, which corresponds to $r = 8$ if only one type of $W_i$ is adapted, $r = 4$ if two are adapted, and $r = 2$ if (all) four are adapted, adapting all four yielded the best training results (followed by two with $r = 4$)

Is the “optimal” adaptation matrix $\Delta W$ really rank-deficient? If so, what is a good rank to use in practice?

Analysis of the normalized subspace similarity between the top $i$ singular vectors in the right-singular unitary matrices (obtained by SVD) of $A_{r=8}$ ($A$ with rank 4) and $A_{r=64}$ demonstrated that the top few directions of $A$ for large and small rank are very highly similar, and thus much of the useful information in $A_{r=64}$ is contained in $A_{r=8}$ and could theoretically be contained in $A$ with rank as low as 1

They suggest that this may indicate that, beyond only a top few directions, $A_{r=64}$ may contain mostly random noises accumulated during training (and performance benchmarks seemed to indicate that gains were somewhat random above even rank 1 or 2 for the tasks assessed)

They support this by comparing two trained $A_{r=64}$ matrices (with different seeds) against the same metric and observing that they are only highly similar for the first few directions

This seems to indicate that a first-pass LoRA FT at a higher rank may be a good way to assess optimal hyperparameter choice of $r$

The authors also suggest that downstream tasks with training data more dissimilar to the original training data, like language acquisition, may require much higher rank decompositions

What is the connection between $\Delta W$ and $W$? Does $\Delta W$ highly correlate with $W$? How large is $\Delta W$ comparing to $W$?

Rephrased in mathematical terms:

is $\Delta W$ mostly contained in the top singular directions of $W$?

They project $W$ onto the top $r$ singular vector $\mathbb{R}^r$ subspaces of $\Delta W$, $W$ (itself, so just $\Sigma$ or SVD), and $R$ a random matrix, by computing $U^\top WV^\top$, where $U$/$V$ are the left/right top $r$ singular-vector matrices of each respective comparison matrix, then compare Frobenius norms: $||A||F = \sqrt{\sum{i,j} a_{i,j}^2}$

First, they observe that $\Delta W$ has a stronger correlation with $W$ than to $R$, indicating that $\Delta W$ amplifies some features already present in $W$

Second, they observe that the Frobenius norm of the projection of $W$ into the subspace of $\Delta W$ is very small, relative to that of its own top $r$ directions, indicating that $\Delta W$ is amplifying directions that are not emphasized in $W$

Third, the amplification factor ($||\Delta W||_F / ||U^\top W V^\top||_F$) of those directions is very large: 21x for $r = 4$

From the paper:

This suggests that the low-rank adaptation matrix potentially amplifies the important features for specific downstream tasks that were learned but not emphasized in the general pre-training model.

This also explains why the minimal necessary rank for $\Delta W$ is so low, but it also suggests that fine-tuning with this method is only feasible if the features required for downstream tasks (or some set of features that compose into them) were already learned during pre-training

Phrased another way, only a sufficiently large model could be fine-tuned with a low rank adaptation in this manner, and smaller models may need larger rank decompositions to compose learned features into downsteam task suitability

Further Research Opportunities

In the LoRA paper, they only adapt the attention weights ($W_q$, $W_k$, $W_v$, $W_o$) and freeze the MLP (feedforward) modules

They also reference Mahabadi et al (2021), which essentially parametrizes the adapter layers using Kronecker products with some predetermined weight sharing scheme, and suggest that

combining LoRA with other tensor product-based methods could potentially improve its parameter efficiency, which we leave to future work